1、 (单选题)如下图所示，在△ABC中，已知AB=AC，AM=AN，∠BAN=30°。问∠MNC的度数是多少?

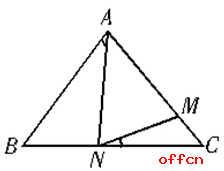
A、15°

B、20°

C、25°

D、30°

1、正确答案【A】

解析：设所求为α，∠B=∠C=∠1，∠ANM=∠AMN=∠2，则可得∠2=∠1+α，α+∠2=∠1+30°，两式左右相减得2α=30°，解得α=15°。

2、 (单选题)有一堆棋子(棋子数大于1)，把它们四等分后剩一枚，拿去三份零一枚，将剩下的棋子再四等分后还是剩一枚，再拿去三份零一枚，将剩下的棋子四等分还是剩一枚。问原来至少多少枚棋子?

A、23

B、37

C、65

D、85

2、正确答案【D】

解析：采用逆推法。最后一次剩下的棋子四等分还剩一枚，则棋子数目至少是5个，则第二次操作前棋子数目至少是5×4+1=21个，第一次操作前棋子数目至少是21×4+1=85个。答案为D。

3、 (单选题)教室里有若干学生，走了10名女生后，男生是女生人数的2倍，又走了9名男生后，女生是男生人数的5倍。问：最初有多少名女生?

A、15

B、12

C、10

D、9

3、正确答案【A】

解析：设最初有x名女生，则男生人数为2×(x-10)，且由题意可知，x-10=5×[2×(x-10)-9]，解得x=15。也可由题意知最初女生人数减去10后是5的倍数，且是一个正整数，结合选项，排除B、C、D项，只能选择A项。走了10名女生，剩下的女生是男生的5倍，可知原有女生人数是5的倍数，选择A。走了10名女生，剩下的女生是男生的5倍，可知原有女生人数是5的倍数，排除B。开始走了10名女生，所以原有女生的数量必定>10，所以排除C项。开始走了10名女生，所以原有女生的数量必定>10，所以排除D项。

4、 (单选题)一位长寿老人生于19世纪90年代，有一年他发现自己年龄的平方刚好等于当年的年份。问这位老人出生于哪一年?

A、1892年

B、1894年

C、1896年

D、1898年

4、正确答案【A】

解析：这位老人生于19世纪90年代，那么“当年”这个年份应该在1890-2000年之间。我们知道40^2=1600,50^2=2500，于是我们可以大胆地在40岁到50岁之间构造老人“当年”的年龄：45^2=2025，很明显，2025年才45岁的人不应该出生在19世纪90年代，排除;44^2=1936，1936年44岁的人应该出生在1936-44=1892年，满足题目条件，所以选A。

5、 (单选题)一项工程，甲单独做，6天可完成;甲乙合做，2天可完成;则乙单独做，_________ 天可完成。

A、1.5

B、3

C、4

D、5

5、正确答案【B】

解析：设这项工程为单位1，则甲的速度为1/6，甲乙共同速度为1/2，那么乙的速度为1/2-1/6=1/3，则乙做完这项工程需要3天。故答案为B。

推荐阅读：

2018湖南招警考试信息汇总

2018年7月湖南招警考试每日一练汇总