在行测数量关系中，有一种特殊题型是错位重排问题，在复习过程中很多人往往没有能够具体学习这个知识点，导致正确率较低。错位重排问题也叫装错信封问题，这是源自于伯努利和欧拉在相互写信过程中所发现的。错装信封问题其实是比较容易做对的，因为它的结论比较简单，所以我们应该重点掌握错位重排的应用环境以及它的结论方法。所以，接下来中公教育专家通过例题来给大家说明如何快速解决错位重排问题。

错位重排问题可以简单的理解为，把n个元素进行重新排列，使得每个元素都不在自己原来对应的位置上。我们通过一个例题来看一下。比如：

例1、现在有三个信封，我们分别用A、B和C表示，分别装有编号为a、b和c的信纸，现在我们把所有信纸重新装进信封，那么所有信纸都没有装进信封的情况有几种?

三封信的情况较为简单。全部装错的情况为：

A B C

(1)b c a

(2)c a b

总共两种情况。

对于类似于上个题目描述的情况，所有元素都不在对应位置上的题目，我们可以判断出此题为错位重排问题。那么我们来分析一下，错位重排问题方法数的规律。其实元素较少的情况下，我们可以通过穷举法来求出结果。比如，当只有一封信(一个信封和一个信纸)的情况下，是不会装错的，也就是说装错的方法数位0;当有2封信的情况下，装错的情况有1种。如：

A B

b a

当有3封信的时候，如例1所示，有2种结果。当有4封信的时候，有9中方法。我们用n表示有多少个元素，用Dn表示n个元素错位重排的方法数，用一个表格写出结果：

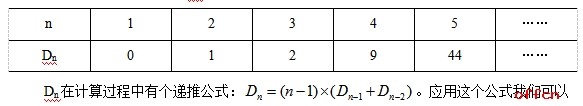
得到其他的情况，但是在考试中上述表格中的数据是常考的，需要我们记住。接下来我们通过两道题目来看一下，错位重排到底如何去应用。